1. 数学定义与运算
正数:大于零的数,表示增加、盈余或正向的量。
负数:小于零的数,表示减少、亏损或反向的量。
对称性:在运算中,正负数互为相反数(如 ( +5 ) 和 ( -5 )),但加减规则不同(如 ( 3 + (-2) = 1 ))。
2. 实际应用中的相反意义
经济领域:
正数代表收入、存款(资产),负数代表支出、欠款(负债)。例如,( +1000 ) 元和 ( -1000 ) 元对财务状况的影响完全相反。
物理方向:
东为正、西为负,或海拔高度中地面以上为正、以下为负。负数表示与正方向相反的位置。
温度计量:
( 10^circ
ext{C} ) 表示零上,( -5^circ
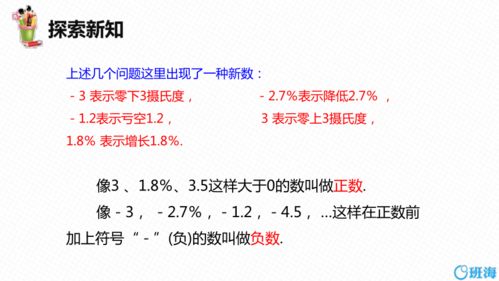
ext{C} ) 表示零下,实际体感温度截然不同。
3. 特殊情况下的意义统一性
数值大小:绝对值相同的正负数(如 ( +5 ) 和 ( -5 ))在表示量的“大小”时相同,但方向相反。例如,移动 ( +5 ) 米和 ( -5 ) 米距离相等,但方向相反。
系统内的相对性:某些场景中正负仅表示相对状态(如电荷的正负),实际作用取决于上下文。
4. 总结
正数和负数在数学上具有运算对称性,但实际意义相反。它们共同描述了一个量的两种对立状态(如盈利/亏损、零上/零下),因此不能简单认为它们的意义相同,而是通过符号区分互为补充的相反概念。理解这一点有助于避免混淆数值大小与实际含义的关系。


