1. 化为标准方程:将椭圆方程整理为以下两种形式之一:
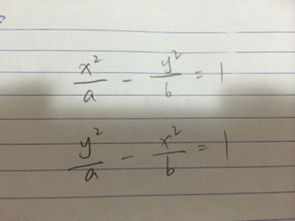
长轴在x轴方向:$frac{(x-h)^2}{a^2} + frac{(y-k)^2}{b^2} =1$(其中 $a > b$)。
长轴在y轴方向:$frac{(x-h)^2}{b^2} + frac{(y-k)^2}{a^2} =1$(其中 $a > b$)。
这里 $(h, k)$ 是椭圆的中心,$a$ 是长半轴,$b$ 是短半轴。
2. 确定参数:
长轴方向通过分母大小判断:分母较大的项对应长轴方向。
若长轴在x轴方向,则 $a$ 为x项分母的平方根;若在y轴方向,则 $a$ 为y项分母的平方根。
3. 计算焦距 $c$:
使用公式 $c = sqrt{a^2
b^2}$,其中 $c$ 为焦点到椭圆中心的距离。
4. 确定焦点坐标:
长轴在x轴方向:焦点坐标为 $(h pm c, k)$。
长轴在y轴方向:焦点坐标为 $(h, k pm c)$。
示例:
方程 $frac{x^2}{25} + frac{y^2}{16} =1$ 中,$a=5$,$b=4$,长轴在x轴方向。计算得 $c=3$,焦点坐标为 $(pm3, 0)$。
方程 $frac{(x+2)^2}{9} + frac{(y-1)^2}{4} =1$ 中心在 $(-2,1)$,长轴在x轴方向,$c=sqrt{5}$,焦点坐标为 $(-2 pm sqrt{5}, 1)$。
通过以上步骤,即可准确求出椭圆的焦点位置。


