在数学理论中,零的相反数仍然是零,不存在“负零”的概念。以下是详细分析:
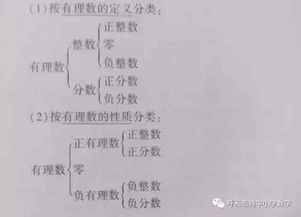
1. 数学定义中的相反数
相反数的定义是:若一个数为 ( a ),其相反数 ( -a ) 满足 ( a + (-a) = 0 )。
对于 ( a = 0 ),代入公式得 ( 0 + (-0) = 0 ),即 ( -0 = 0 )。数学上 ( 0 ) 的相反数是它本身,没有“正零”和“负零”的区分。
2. 计算机科学中的“负零”
在计算机的浮点数表示(如IEEE 754标准)中,零可能被区分为 (+0) 和 (-0)。这种设计是为了保留符号信息,例如:
(1.0 / +infty rightarrow +0)
(1.0 / -infty rightarrow -0)
但在数值运算中,(+0) 和 (-0) 是相等的(即 ( +0 = -0 )),区别仅在于某些特殊场景(如极限方向)中符号可能影响结果。
3. 数学与计算机的边界
在纯数学领域,零是一个无符号的数,其相反数只能是自身。
在计算机应用中,负零是表示方式的问题,不改变零的实际值。
若问题基于数学理论,答案是否定的:零的相反数只能是零本身。若涉及计算机科学或工程应用,负零是存在的技术概念,但其数值仍等于零,符号仅用于特定场景的处理。


