什么是正数负数自然数
摘要:1. 正数
定义:大于零的实数,符号通常省略或写作“+”。
例子:3, +5, 2.718, 1/2。
特点:在数轴上位于零的右侧,表示具有“正值”的量,如收入、温度升高等。
2. 负数
定
1. 正数
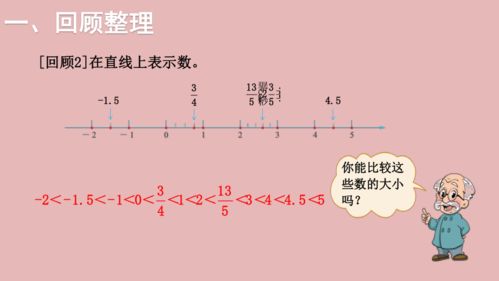
定义:大于零的实数,符号通常省略或写作“+”。
例子:3, +5, 2.718, 1/2。
特点:在数轴上位于零的右侧,表示具有“正值”的量,如收入、温度升高等。
2. 负数
定义:小于零的实数,符号为“-”。
例子:-3, -5, -π, -0.5。
特点:数轴上位于零的左侧,表示相反意义,如欠款、温度下降等。
注意:零既不是正数也不是负数。
3. 自然数
定义争议:
包含零的情况(常见于*论、计算机科学):0, 1, 2, 3, …
不包含零的情况(常见于数论、传统数学教材):1, 2, 3, …
特点:非负整数(或正整数),用于计数或排序。
例子:
含零:0个苹果、1棵树、2本书。
不含零:第1名、2个选项、3次尝试。
总结区别:
正数和负数基于与零的关系划分,且均为实数;自然数则是整数的子集,可能包含或不含零。
关键点:自然数的定义需结合上下文,但现代数学(如国际标准ISO 80000-2)通常包含零。
通过理解这三个概念,可以更清晰地分析数学问题中的数值属性。


