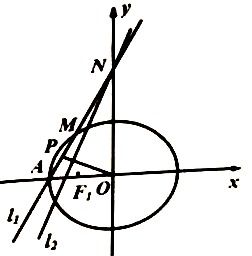
椭圆焦点长轴短轴的性质

2025-05-14 #长轴 #椭圆 #性质 #焦点阅读量：3

1. 焦点 (Foci)

位置：两个焦点 ( F_1 ) 和 ( F_2 ) 位于长轴上，对称分布于椭圆中心两侧，距离中心的距离为 ( c )，满足 ( c^2 = a^2

b^2 )（( a ) 为半长轴，( b ) 为半短轴）。

几何意义：椭圆上任意一点到两个焦点的距离之和恒为 ( 2a )，即 ( PF_1 + PF_2 = 2a )。

定义：椭圆的最长直径，长度为 ( 2a )，方向决定了椭圆的延伸方向。

顶点：长轴的两个端点称为顶点，坐标为 ( (pm a, 0) )（假设长轴在x轴上）。

半长轴：长度 ( a ) 是椭圆中心到顶点的距离，也是椭圆的标准方程参数之一。

定义：与长轴垂直的最短直径，长度为 ( 2b )，其中 ( b ) 为半短轴。

端点：短轴端点坐标为 ( (0, pm b) )（假设长轴在x轴上）。

几何关系：短轴的端点到两个焦点的距离之和同样为 ( 2a )。

长轴在x轴上：( frac{x^2}{a^2} + frac{y^2}{b^2} = 1 )

长轴在y轴上：( frac{x^2}{b^2} + frac{y^2}{a^2} = 1 )

定义：( e = frac{c}{a} = frac{sqrt{a^2

b^2}}{a} )，且 ( 0 < e < 1 )。

几何意义：离心率反映椭圆的扁平程度。( e ) 越接近1，椭圆越扁；( e=0 ) 时椭圆退化为圆。

椭圆关于长轴、短轴和中心对称，对称性由焦点和轴的位置决定。

( c^2 = a^2

b^2 )

( e = frac{c}{a} )

焦点坐标（长轴在x轴上）：( (pm c, 0) )

这些性质共同描述了椭圆的几何特征，广泛应用于天文学（行星轨道）、光学（镜面反射）等领域。

椭圆焦点长轴短轴的性质