椭圆的两个焦点是椭圆上的关键点,决定了椭圆的形状和性质。焦距则是与焦点相关的重要参数,具体解释如下:
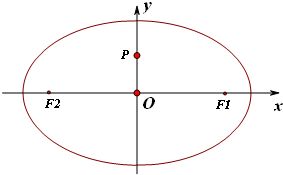
1. 焦点(Foci)
定义:椭圆的两个焦点(通常记作 ( F_1 ) 和 ( F_2 ))是位于椭圆长轴上的两个固定点,对称分布在椭圆中心两侧。
重要性:椭圆上任意一点到这两个焦点的距离之和为常数,且等于椭圆的长轴长度 ( 2a )(( a ) 是长半轴)。这是椭圆的定义性质,即:
[
PF_1 + PF_2 = 2a quad (
ext{其中 } P
ext{ 是椭圆上的任意一点})
]
2. 焦距
焦距有两种常见定义,需注意区分:
焦点到中心的距离(( c )):每个焦点到椭圆中心的距离称为 焦距,记为 ( c )。它与长半轴 ( a ) 和短半轴 ( b ) 满足关系:
[
c^2 = a^2
b^2
]
两焦点间的距离:有时“焦距”也指两焦点 ( F_1F_2 ) 之间的距离,即 ( 2c )。
3. 几何意义
椭圆的扁平程度:焦距 ( c ) 越大,椭圆越扁;当 ( c=0 ) 时,焦点与中心重合,椭圆变为圆。
离心率 ( e ):描述椭圆的扁平程度,定义为 ( e = frac{c}{a} )(( 0 leq e < 1 ))。离心率越大,椭圆越扁。
4. 示例
假设椭圆的长半轴 ( a=5 ),短半轴 ( b=3 ),则:
[
c = sqrt{a^2
b^2} = sqrt{25
9} = 4
]
焦点到中心的距离为 ( 4 )。
两焦点间距为 ( 8 )。
5. 应用
天体轨道:行星绕太阳的轨道是椭圆,太阳位于一个焦点。
光学:椭圆镜面可将从一个焦点发出的光反射到另一个焦点。
通过理解焦点和焦距,可以更深入地掌握椭圆的几何特性和实际应用。


