椭圆的焦距和焦点是什么意思啊

2025-05-19 阅读 3 评论 0

摘要：椭圆的焦点和焦距是其重要的几何特征，具体解释如下：
焦点（Foci）
定义：椭圆的两个焦点（记为 ( F_1 ) 和 ( F_2 )）是位于椭圆长轴上的两个固定点。椭圆上任意一点到这两个焦点的距离

椭圆的焦点和焦距是其重要的几何特征，具体解释如下：

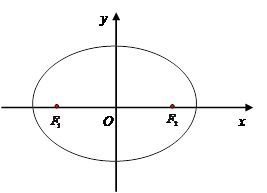
椭圆的焦距和焦点是什么意思啊

焦点（Foci）

定义：椭圆的两个焦点（记为 ( F_1 ) 和 ( F_2 )）是位于椭圆长轴上的两个固定点。椭圆上任意一点到这两个焦点的距离之和恒等于椭圆的长轴长度 ( 2a )（( a ) 为半长轴）。

位置：焦点位于长轴上，距离椭圆中心 ( O ) 的距离为 ( c )，坐标分别为 ( (pm c, 0) )（长轴在x轴时）或 ( (0, pm c) )（长轴在y轴时）。

定义：焦距通常指两个焦点之间的距离，即 ( 2c )。其中 ( c ) 是单个焦点到椭圆中心的距离。

公式：焦距与半长轴 ( a ) 和半短轴 ( b ) 满足关系 ( c^2 = a^2

b^2 )。焦距 ( 2c = 2sqrt{a^2 - b^2} )。

1. 离心率：定义为 ( e = frac{c}{a} )，取值范围为 ( 0 < e < 1 )。离心率越大，椭圆越扁平；当 ( e

o 0 ) 时，椭圆接近圆形。

2. 形状影响：( c ) 越大（即焦距越大），椭圆越扁；当 ( c = 0 ) 时，焦点重合于中心，椭圆变为圆。

若椭圆方程为 ( frac{x^2}{25} + frac{y^2}{9} = 1 )，则 ( a = 5 )，( b = 3 )，计算得 ( c = sqrt{25

9} = 4 )。焦距为 ( 2c = 8 )，焦点坐标为 ( (pm 4, 0) )。

焦点决定了椭圆的形状，而焦距反映了椭圆的扁平程度。理解这两个概念有助于分析椭圆的性质及其几何应用。

标签：焦距椭圆意思焦点