1. 标准方程形式:
主轴在x轴:(frac{(x-h)^2}{a^2} + frac{(y-k)^2}{b^2} = 1)((a > b))
主轴在y轴:(frac{(x-h)^2}{b^2} + frac{(y-k)^2}{a^2} = 1)((a > b))
中心坐标为((h, k)),长半轴为(a),短半轴为(b)。
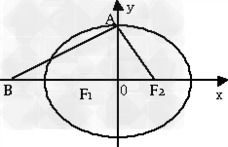
2. 焦点与顶点的位置:
顶点:位于长轴上,距中心(a)个单位。主轴在x轴时顶点为((h pm a, k));主轴在y轴时为((h, k pm a))。
焦点:位于长轴上,距中心(c)个单位,满足(c = sqrt{a^2
b^2})。焦点坐标为主轴方向移动(c),例如主轴在x轴时为((h pm c, k)),y轴时为((h, k pm c))。
示例:
若椭圆中心在原点,焦点在(±3, 0),顶点在(±5, 0):
(a = 5),(c = 3),计算得(b = sqrt{a^2
c^2} = 4)。
方程:(frac{x^2}{25} + frac{y^2}{16} = 1)。
答案:
椭圆的顶点位于长轴端点,焦点位于长轴上距中心(c = sqrt{a^2
b^2})处。例如,中心在原点、焦点在(±3,0)且顶点在(±5,0)的椭圆方程为:
[
boxed{frac{x^2}{25} + frac{y^2}{16} = 1}
]
顶点坐标为(±5, 0),焦点坐标为(±3, 0)。


